Sedangkan bentuk umum dari fungsi kuadrat adalah:
Dengan a, b, merupakan koefisien, dan c adalah konstanta, serta
Fungsi kuadrat f(x) dapat juga ditulis dalam bentuk y atau:
Dengan x adalah variable bebas dan y adalah variable terikat. Sehingga nilai y tergantung pada nilai x, dan nilai-nilai x tergantung pada area yang ditetapkan. Nilai y diperoleh dengan memasukan nilai-nilai x kedalam fungsi.
Grafik Fungsi Kuadrat
Fungsi kuadrat  dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
dapat digambarkan ke dalam koordinat kartesius sehingga diperoleh suatu grafik fungsi kuadrat. Sumbu x adalah domain dan sumbu y adalah kodomain. Grafik dari fungsi kuadrat berbentuk seperti parabola sehingga sering disebut grafik parabola.
Grafik dapat dibuat dengan memasukan nilai x pada interval tertentu sehingga didapat nilai y. Kemudian pasangan nilai (x, y) tersebut menjadi koordinat dari yang dilewati suatu grafik. Sebagai contoh, grafik dari fungsi: 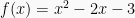 adalah:
adalah:

Jenis grafik fungsi kuadrat lain
1. Grafik fungsi 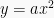
Jika pada fungsi  memiliki nilai b dan c sama dengan nol, maka fungsi kuadratnya:
memiliki nilai b dan c sama dengan nol, maka fungsi kuadratnya:
Pada grafik fungsi ini akan selalu memiliki garis simetris pada x = 0 dan titik puncak y = 0. Sebagai contoh 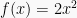 , maka grafiknya adalah:
, maka grafiknya adalah:

2. Grafik fungsi 
Jika pada fungsi  memiliki nilai b = 0, maka fungsi kuadratnya sama dengan:
memiliki nilai b = 0, maka fungsi kuadratnya sama dengan:
Pada fungsi ini grafik akan memiliki kesamaan dengan grafik fungsi kuadrat 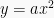 yaitu selalu memiliki garis simetris pada x = 0. Namun, titik puncaknya sama dengan nilai c atau
yaitu selalu memiliki garis simetris pada x = 0. Namun, titik puncaknya sama dengan nilai c atau 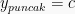 . Sebagai contoh =
. Sebagai contoh =  + 2, maka grafiknya adalah:
+ 2, maka grafiknya adalah:

3. Grafik fungsi 
Grafik ini merupakan hasil perubahan bentuk dari  . Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut:
. Pada fungsi kuadrat ini grafik akan memiliki titik puncak (x, y) sama dengan (h, k). Hubungan antara a, b, dan c dengan h, k sebagai berikut:
Sifat-sifat Grafik Fungsi Kuadrat
a. Grafik terbuka
Grafik  dapat terbuka ke atas atau ke bawah. Sifat ini ditentukan oleh nilai a. Jika
dapat terbuka ke atas atau ke bawah. Sifat ini ditentukan oleh nilai a. Jika 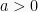 maka grafik terbuka ke atas, jika
maka grafik terbuka ke atas, jika  maka grafik terbuka kebawah.
maka grafik terbuka kebawah.

b. Titik Puncak
Grafik kuadrat mempunyai titik puncak atau titik balik. Jika grafik terbuka kebawah, maka titik puncak adalah titik maksimum. Jika grafik terbuka keatas maka, titik puncak adalah titik minimum.
c. Sumbu Simetri
Sumbu simetri membagi grafik kuadrat menjadi 2 bagian sehingga tepat berada di titik puncak. Karena itu, letaknya pada grafik  berada pada:
berada pada:
d. Titik potong sumbu y
Grafik  memotong sumbu y di x = 0. Jika nilai x = 0 disubstitusikan ke dalam fungsi, diperoleh y = c. Maka titik potong berada di (0, c).
memotong sumbu y di x = 0. Jika nilai x = 0 disubstitusikan ke dalam fungsi, diperoleh y = c. Maka titik potong berada di (0, c).

e. Titik potong sumbu x
Grafik kuadrat akan memotong sumbu x di y = 0, sehingga membentuk persamaan:
Akar-akar dari persamaan tersebut adalah absis dari titik potong. Oleh karena itu, nilai diskriminan (D) berpengaruh pada keberadaan titik potong sumbu x sebagai berikut:
- Jika
, grafik memotong sumbu x di dua titik
- Jika
, grafik menyinggung sumbu x
- Jika
, grafik tidak memotong sumbu x
Jika digambarkan, sebagai berikut:

Menyusun Persamaan Grafik Fungsi Kuadrat
Persamaan grafik fungsi kuadrat dapat dibentuk dengan syarat:
- Diketahui tiga titik koordinat (x, y) yang dilalui oleh grafik
Ketiga koordinat tersebut, masing-masing disubstitusikan kedalam persamaan grafik:
Sehingga didapat tiga persamaan berbeda yang saling memiliki variabel a, b dan c. Selanjutnya dilakukan teknik eliminasi aljabar untuk memperoleh nilai dari a, b dan c. Setelah diperoleh nilai-nilai itu, kemudian masing-masing disubstitusikan ke dalam persamaan  sebagai koefisien.
sebagai koefisien.
- Diketahui titik potong dengan sumbu x dan satu titik yang dilalui
Jika titik potong sumbu x adalah 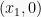 dan
dan 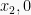 , maka rumus fungsi kuadrat nya adalah:
, maka rumus fungsi kuadrat nya adalah:
Dengan nilai a didapat dari mensubstitusikan titik (x, y) yang dilalui.
- Diketahui titik puncaknya dan satu titik yang dilalui
Jika titik puncaknya adalah 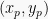 , maka rumus fungsi kuadrat nya adalah:
, maka rumus fungsi kuadrat nya adalah:
Dengan nilai a didapat dari mensubstitusikan titik (x, y) yang dilalui.
Contoh Soal Fungsi Kuadrat dan Pembahasan
Contoh Soal 1
Jika grafik  mempunyai titik puncak (1, 2), tentukan nilai a dan b. (UMPTN ’92)
mempunyai titik puncak (1, 2), tentukan nilai a dan b. (UMPTN ’92)
Pembahasan 1:
Gunakan rumus 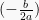 sebagai nilai x titik puncak, sehingga:
sebagai nilai x titik puncak, sehingga:
Substitusi titik puncak (1, 2) ke dalam persamaan  diperoleh:
diperoleh:
Dari persamaan baru, substitusikan nilai  ,maka:
,maka:
Contoh Soal 2
Jika fungsi 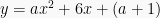 mempunyai sumbu simetri x = 3, tentukan nilai maksimumnya. (UMPTN ‘00)
mempunyai sumbu simetri x = 3, tentukan nilai maksimumnya. (UMPTN ‘00)
Pembahasan:
Sumbu simetri berada di x titik puncak, sehingga:
Sehingga fungsi y menjadi:
Nilai maksimumnya:
Soal 3
Tentukan grafik yang melintasi (-1, 3) dan titik minimumnya sama dengan puncak grafik 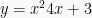 . (UMPTN ‘00)
. (UMPTN ‘00)
Pembahasan:
Titik puncak  adalah:
adalah:
Substitusikan nilai 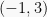 dan
dan 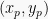 dalam persamaan:
dalam persamaan:
Maka grafik fungsi kuadrat yang dicari adalah:
Video pembelajaran Fungsi Kuadrat
Sumber materi: www.studiobelajar.com/fungsi-kuadrat/.
Novita aulia XI Otkp5
BalasHapusDelisahara XI Otkp 3
BalasHapusSri Rahayu
BalasHapusXl oktp 6
Murni Safitri XI OTKP 4
BalasHapusFawadz Abdul Azis XI OTKP 5 HADIR 🙏
BalasHapusMuhammad Rakha Triana nur Otkp 1
BalasHapusIka jayanti 11 otkp 01
BalasHapusMuhamad Rizky XI OTKP 6 hadir
BalasHapusRika rahmawati dewi 11 otkp 1
BalasHapusRika rahmawati dewi 11 otkp 1
BalasHapusNovia dwi aryani XI-OTKP_8 hadir
BalasHapusRahmi Widiantari XI OTKP 2
BalasHapusRahmi Widiantari XI OTKP 2
BalasHapusEneng siti rohayati r XI otkp 4
BalasHapusHadir
BalasHapusLia Amelia XI Otkp 3
BalasHapusTia wati XI otkp 2
BalasHapusAriyanti Xl Otkp 1
BalasHapusHerawati saputri XI Otkp 4
BalasHapusMuhammad Rizki Waluya Otkp 1
BalasHapusNama sandi irpansah otkp 1 pak
BalasHapusSri julianti Xl otkp 7
BalasHapusAnisa rahmawati XI otkp 3
BalasHapusAnisa rahmawati XI otkp 3
BalasHapusDita Maziyatul Aulia, XI OTKP 6. Hadir pak
BalasHapusLia Rahmawati XI Otkp 4
BalasHapusSITI NURLELA XI OTKP 1
BalasHapusMa'mun nawawi XI Otk 2
BalasHapusSiti Irmayanti XI OTKP 5 Hadir
BalasHapusVida putri xi otkp 5 hadir
BalasHapusEneng meisya rusliawati Xl otkp 2 hadir
BalasHapusTaufik Hidayatullah Xl OTKP 8 Hadir
BalasHapusPinkan Nourisna Erlian D
BalasHapus11 otkp 8
Frisda Damayanti Septiani XI Otkp 3
BalasHapusSyahlan Widi rizky XI OTKP 1 hadir
BalasHapusAssalamualaikum
BalasHapusFina tania XI otkp 6
Dian safitri XI otkp 5 hadir
BalasHapusQannia Friza Yasmita (XI OTKP 3)
BalasHapusSilmi Aziz XI OTKP 3
BalasHapusMuhammad Aldi mardiansyah
BalasHapusXI otkp 8
Muhamad Ramlan XI OTkp 6
BalasHapusMeta Ainanda XI OTKP 5
BalasHapusRifky DwiPutra Fernanda
BalasHapusXI otkp 1 hadirr
U.Misjan XI OTKP 5
BalasHapusGladys marshanda XIotkp1
BalasHapusAssalamualaikum,
BalasHapusAyang Oktapiani
Kelas XI OTKP 5
M.abdul karim
BalasHapusXI-OTKP 7
Riska Amanda Lestari
BalasHapusXI Otkp5 Hadir
Fitriani. Xl Otkp 3 hadir
BalasHapusRaivan Vudiansyah
BalasHapusXI OTKP 03
Hadir
Nurul Annisa XI otkp 5
BalasHapusSennita Sari
BalasHapusXI OTKP 2
Komentar ini telah dihapus oleh pengarang.
BalasHapusRestu Febriyanti XI OTKP 4
BalasHapusZakaria XI otkp 8
BalasHapusMuhammad Rakha Triana nur xI ap1
BalasHapus