Pengertian Turunan
Turunan adalah pengukuran terhadap bagaimana fungsi berubah seiring perubahan nilai yang dimasukan, atau secara umum turunan menunjukkan bagaimana suatu besaran berubah akibat perubahan besaran lainnya. Proses dalam menemukan turunan disebut diferensiasi.
Pada fungsi y = f(x), turunan dari variabel y terhadap variabel x dinotasikan dengan  atau
atau 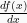 atau y’ dan didefinisikan sebagai:
atau y’ dan didefinisikan sebagai:
Rumus-rumus Turunan Fungsi Aljabar
Dengan definisi turunan akan dicari rumus-rumus turunan fungsi aljabar yang terdiri dari fungsi pangkat  , hasil kali fungsi f(x) = u(x) . v(x), hasil pembagian fungsi
, hasil kali fungsi f(x) = u(x) . v(x), hasil pembagian fungsi  , dan pangkat dari fungsi
, dan pangkat dari fungsi  .
.
1. Rumus turunan fungsi pangkat 
Fungsi berbentuk pangkat turunannya dapat menggunakan rumus 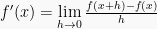 sebagai:
sebagai:
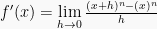

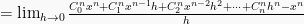
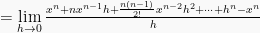

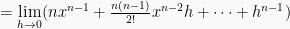
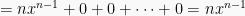
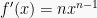
2. Rumus turunan hasil kali fungsi
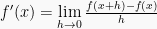
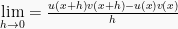

![=\lim\limits_{h\to0}\frac{[u(x+h)v(x+h)-u(x+h)v(x)]+[u(x+h)v(x)-u(x)v(x)]}{h} =\lim\limits_{h\to0}\frac{[u(x+h)v(x+h)-u(x+h)v(x)]+[u(x+h)v(x)-u(x)v(x)]}{h}](https://s0.wp.com/latex.php?latex=%3D%5Clim%5Climits_%7Bh%5Cto0%7D%5Cfrac%7B%5Bu%28x%2Bh%29v%28x%2Bh%29-u%28x%2Bh%29v%28x%29%5D%2B%5Bu%28x%2Bh%29v%28x%29-u%28x%29v%28x%29%5D%7D%7Bh%7D&bg=f9f9f9&fg=000000&s=0)
![= \lim \limits_{h\to0}\frac{u(x+h)[v(x+h)-v(x)]}{h}+\lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)}{h} = \lim \limits_{h\to0}\frac{u(x+h)[v(x+h)-v(x)]}{h}+\lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)}{h}](https://s0.wp.com/latex.php?latex=%3D+%5Clim+%5Climits_%7Bh%5Cto0%7D%5Cfrac%7Bu%28x%2Bh%29%5Bv%28x%2Bh%29-v%28x%29%5D%7D%7Bh%7D%2B%5Clim+%5Climits_%7Bh%5Cto0%7D%5Cfrac%7B%5Bu%28x%2Bh%29-u%28x%29%5Dv%28x%29%7D%7Bh%7D&bg=f9f9f9&fg=000000&s=0)



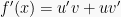
3. Rumus turunan fungsi pembagian
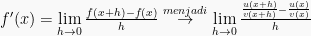
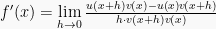

![= \lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)-u(x)[v(x+h)-v(x)]}{h.v(x+h)v(x)} = \lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)-u(x)[v(x+h)-v(x)]}{h.v(x+h)v(x)}](https://s0.wp.com/latex.php?latex=%3D+%5Clim+%5Climits_%7Bh%5Cto0%7D%5Cfrac%7B%5Bu%28x%2Bh%29-u%28x%29%5Dv%28x%29-u%28x%29%5Bv%28x%2Bh%29-v%28x%29%5D%7D%7Bh.v%28x%2Bh%29v%28x%29%7D&bg=f9f9f9&fg=000000&s=0)
![= \lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)}{h \cdot v(x+h)v(x)} - \lim \limits_{h\to0}\frac{u(x)[v(x+h)-v(x)]}{h \cdot v(x+h)v(x)} = \lim \limits_{h\to0}\frac{[u(x+h)-u(x)]v(x)}{h \cdot v(x+h)v(x)} - \lim \limits_{h\to0}\frac{u(x)[v(x+h)-v(x)]}{h \cdot v(x+h)v(x)}](https://s0.wp.com/latex.php?latex=%3D+%5Clim+%5Climits_%7Bh%5Cto0%7D%5Cfrac%7B%5Bu%28x%2Bh%29-u%28x%29%5Dv%28x%29%7D%7Bh+%5Ccdot+v%28x%2Bh%29v%28x%29%7D+-+%5Clim+%5Climits_%7Bh%5Cto0%7D%5Cfrac%7Bu%28x%29%5Bv%28x%2Bh%29-v%28x%29%5D%7D%7Bh+%5Ccdot+v%28x%2Bh%29v%28x%29%7D&bg=f9f9f9&fg=000000&s=0)




4. Rumus turunan pangkat dari fungsi
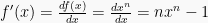
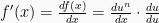
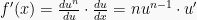
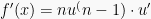
Jadi rumus turunan fungsi pangkat adalah:
2. Rumus turunan hasil kali fungsi 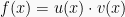
Fungsi f(x) yang terbentuk dari perkalian fungsi u(x) dan v(x), turunannya didapat dengan:
Jadi rumus turunan fungsinya adalah:
3. Rumus turunan fungsi pembagian 
sehingga
Jadi rumus turunan fungsinya adalah
4. Rumus turunan pangkat dari fungsi 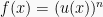
Ingat jika  , maka:
, maka:
Karena 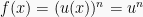 , maka:
, maka:
Atau
Jadi rumus turunan fungsinya adalah:
Sumber: www.studiobelajar.com
Rima Efendi hadir
BalasHapusTia wati kelas XI otkp 2
BalasHapusLia Rahmawati XI Otkp 4
BalasHapusSindi Aulia XI OTKP 4
BalasHapusMuhammad Rizki Waluya OTKP 1
BalasHapusAriyanti Xl Otkp 1
BalasHapusHerawati saputri XI Otkp 4
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusAnisa XI OTKP 2
BalasHapusNuraini Saputri 11 Otkp 1
BalasHapusFrisda Damayanti Septiani XI Otkp 3
BalasHapusSoni kurniawan XI Otkp2 Hadir
BalasHapusSITI MUNAWAROH XI OTKP6
BalasHapusAsyifa aulia p XI ap1
BalasHapusMurni Safitri XI OTKP 4
BalasHapusMuhamad ikbal Bahrudin otkp5
BalasHapusSiti NurLela XI Otkp1 hadir
BalasHapusNovia dwi aryani XI-OTKP_8 hadirr
BalasHapusSri Rahayu
BalasHapusXl Otkp 6
Hadirr
Novita aulia XI otkp5
BalasHapusMelisa XI Otkp 1
BalasHapusEneng siti rohayati rukmini XI otkp 4 hadir
BalasHapusAyuni XI OTKP-2
BalasHapusAyuni XI OTKP-2
BalasHapusAssalamualaikum ma'mun mawawi XI otkp 2
BalasHapusFitri andini shabrillah bugis Xl otkp 6
BalasHapusDita Maziyatul Aulia, XI OTKP 6. Hadir pak
BalasHapusLia Amelia XI Otkp 3
BalasHapusSilmi Aziz XI OTKP 3 Hadir
BalasHapusIndah puji hardiyanti XI otkp 2
BalasHapusEDOBUDIYANTO OTKP-3 xI hadir
BalasHapusSintia Ningrum Mandasari XI OTKP 3
BalasHapusFawadz Abdul Azis XI OTKP 5 HADIR
BalasHapusRifky DwiPutra Fernanda
BalasHapusXI OTKP 1 hadirr
Silviani komalasari XI Otkp3
BalasHapusCian Purbasari XI OTKP 2
BalasHapusSilviani komalasari XI Otkp3
BalasHapusAisyah otkp6
BalasHapusYanti Nurhayati Otkp3
BalasHapusMirna Wati
BalasHapusXI-OTKP 2
Muhammad Ardiansyah
BalasHapusXI OTKP 3
Yudi XI OTKP 1 hadir
BalasHapusMuhamad Rizky XI OTKP 6 hadir
BalasHapusFera khairani XI otkp 8 hadir
BalasHapusSunarya XI otKP 1 hadir
BalasHapusTaufik Hidayatullah Xl OTKP 8 Hadir pak
BalasHapusNurul Annisa XI otkp 5
BalasHapusSri julianti Xl otkp 7 hadir
BalasHapusNeng Yusabana Mubina XI OTKP 8
BalasHapusSandi irfansyah
BalasHapusXI otkp 1
Rian indriyani xl otkp2
BalasHapusUlfah Azzahra otkp 4 hadirrroohhh
BalasHapusYudis XI Otkp 4
BalasHapusRika Oktavia Silitonga XI OTKP 1
BalasHapusIka jayanti 11 otkp 01
BalasHapusSiti Nopiyanti XI OTKP 6
BalasHapusLarasandra seviani XI OTKP 5
BalasHapuselfiana savira m xl otkp 4
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusRaivan Vudiansyah
BalasHapusXI OTKP 03 hadir
Salsa Sakila Septiani XI Otkp 1
BalasHapusMuhamnad aldi XI otkp 8 hadirr
BalasHapusDian Safitri XI otkp 5 hadir
BalasHapusVida putri XI OTKP 5 HADIR
BalasHapusRika rahmawati dewi 11otkp1
BalasHapusMoch Reza Aditya XI Otkp4 hadir pak
BalasHapusRika rahmawati dewi 11otkp1
BalasHapusZilda f otkp 7 hadir
BalasHapusHasanudin XI OTKP 3
BalasHapusSennita Sari
BalasHapusXI OTKP 2
Anisa Rahmawati
BalasHapusXI otkp 3
Pinkan nourisna erlian dini
BalasHapus11 otkp 8
Meylani Angelina Putri XI Otkp 1
BalasHapusRestu Febriyanti XI OTKP 4
BalasHapusEneng meisya rusliawati XI otkp 2 hadir pa
BalasHapusQannia Friza Yasmita (XI OTKP 3)
BalasHapusSiti Irmayanti OKTP 5 Hadir
BalasHapusGladys marshanda XI otkp1
BalasHapusAnanda Nurlaely 11 otkp 8 hadiirr
BalasHapusNeng Yusabana Mubina XI OTKP 8
BalasHapusKomentar ini telah dihapus oleh pengarang.
BalasHapusMaryansi pfr
BalasHapusXI otkp 3
Deli Sahara Xl Otkp 3
BalasHapusRima Efendi XI OTKP 6
BalasHapusMeta Ainanda XI OTKP 5
BalasHapusDebi Amalia Rinjani
BalasHapusXl otkp 5
Debi Amalia Rinjani
BalasHapusXl otkp 5
M. Abdul Karim XI-OTKP 7
BalasHapusMuhammad Rifky Hidayat XI otkp 5
BalasHapusSopi nadia XI oktp 3 hadir
BalasHapusSiti munjilah XI OTKP 8
BalasHapus